Introduction to Language Models and Inference

Graham Neubig

Carnegie Mellon University Language Technologies Institute

Language Models Permeate Our Lives

  • General Assistants: ChatGPT, Google Search
  • Code Completion: Copilot, Cursor
  • Coding Agents: Codex, Jules, OpenHands
  • Specialized Apps: Harvey (Legal), Abridge (Medical)
  • etc. etc.

What Is a Language Model?

  • A model that assigns probabilities to sequences of tokens
  • \(P(x)\) for a sequence \(x = x_1, x_2, \ldots, x_L\)
  • Most common: autoregressive models
    • \(P(x) = P(x_1) P(x_2 \mid x_1) P(x_3 \mid x_{\lt 3}) \ldots P(x_L \mid x_{\lt L})\)
  • Some counter-examples: energy-based models/diffusion models

Example: Unconditioned Completions

Generated from BOS token (Qwen3-1.7B-Base):

  • Highest Probability:
    • “3.” (-4.22)
    • “4.” (-4.50)
    • “0)” (-7.01)
  • Middle Probability:
    • “8 \text{ dollars} - 5 \text{ dollars} = 3 \text{ dollars}” (-20.31)
    • “3 \) because \( 2^3 = 8 \) and \( 2^{-3} = \frac{1}{8} \” (-22.53)
    • “1) = (x + 2) - (x + 1) = 1” (-23.03)
  • Lowest Probability:
    • “2015—2016 学年度下学期期末统考 高三文科数学 2016．06” (-35.62)
    • “为深入贯彻落实关于党史学习教育"办实事、开新局"的要求，按照公司党委关于党史学习教育的部署，7月6日，公司” (-47.32)
    • “本篇博文主要针对在使用MySQL数据库进行数据库操作时遇到的问题进行记录和总结。包括：” (-56.30)

Conditional Probability

  • Often we want \(P(x_{\ge n} \mid x_{\lt n})\)
    • Also written as \(P(y \mid x)\)
  • \(x_{\lt n}\) (or \(x\)) is the prefix or query
  • \(x_{\ge n}\) (or \(y\)) is the completion or response
  • Mathematically, omit the first \(n\) tokens of \(x\) in the product:
    • \(P(x_{\ge n} \mid x_{\lt n}) = P(x_{n} \mid x_{\lt n}) P(x_{n+1} \mid x_{\lt n+1}) \ldots P(x_{L} \mid x_{\lt L})\)

Example: Conditional Completions

Prompt: “The best thing about Carnegie Mellon University is”

  • Highest Probability:
    • " its diversity." (-5.00)
    • " that it’s a community." (-9.87)
  • Middle Probability:
    • " its location and the vibrant community it has built." (-18.13)
    • " that there’s always something else to learn." (-18.50)
    • " that it gives you the ability to take your education to the next level." (-20.02)
  • Lowest Probability:
    • " its focus on the interdisciplinary approach, with students majoring in computer science, mathematics and engineering." (-38.92)
    • " the community that you get in it, with so many people doing so many different things." (-39.69)
    • " not just its academics and research in engineering, computer science and business — it’s the amazing, out-of-the ordinary experiences your students create in the classroom" (-68.35)

Modeling

  • How to model \(P(x_n \mid x_{\lt n})\)?
  • Typically Transformer models
  • Other options exist, e.g. MoEs, RNNs, or Mamba
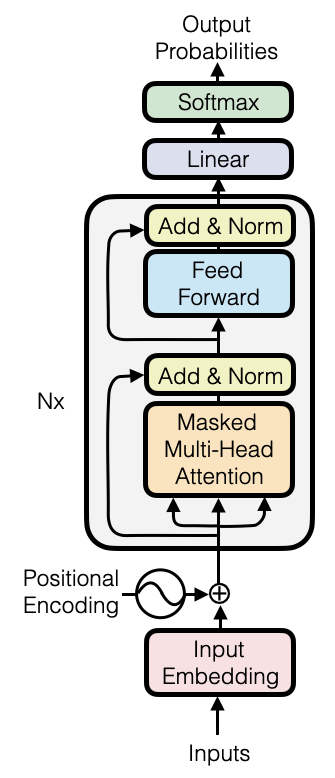
Transformer Architecture

Modeling Cost

  • Self-attention: quadratic in sequence length \(L\)
  • Feed-forward layers (FFN): wide and heavy
  • \(N\) layers: total cost scales linearly with \(N\)
Transformer Architecture

FLOPs per Layer (GQA Transformer)

  • Variables: \(L\) (tokens), \(d\) (hidden size), \(H\) (heads), \(H_{kv}\) (KV heads), \(d_h = d/H\), \(d_{ff}\) (FFN size)
  • Self-attention FLOPs per layer (with GQA):

\[\underbrace{2L\,d^2}_{\text{Q proj}} +\underbrace{2L\,d \cdot H_{kv} d_h}_{\text{K proj}} +\underbrace{2L\,d \cdot H_{kv} d_h}_{\text{V proj}} +\underbrace{4H\,L^2\,d_h}_{QK^T + AV} +\underbrace{2L\,d^2}_{\text{output proj}}\]

  • Feed-forward FLOPs per layer (SwiGLU):

\[\underbrace{2L\,d\,d_{ff}}_{\text{gate}} +\underbrace{2L\,d\,d_{ff}}_{\text{up}} +\underbrace{2L\,d_{ff}\,d}_{\text{down}}\]

e.g. Llama-3.1 Series

Model Parameters Layers Hidden Size Attention Heads KV Heads MLP Size
Llama-3.1-8B 8.0B 32 4,096 32 8 14,336
Llama-3.1-70B 70.6B 80 8,192 64 8 28,672
Llama-3.1-405B 405.9B 126 16,384 128 8 53,248

(source: Hugging Face 1, 2, 3 )

FLOPs vs Context Length

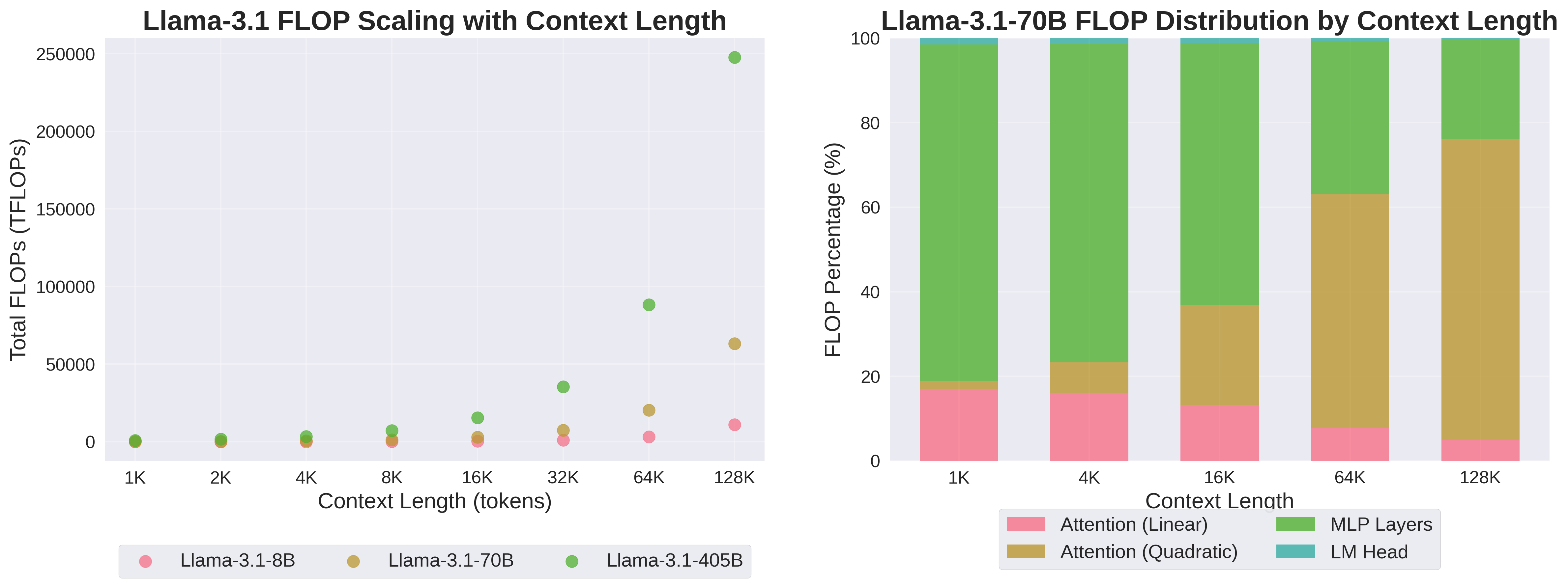
FLOP Scaling Analysis

  • Total FLOPs scale quadratically with context
  • MLP dominates for short sequences, attention for long

Hardware

  • CPU: General-purpose, but typically too slow for LLMs
  • NVIDIA GPU: Parallel processing, high memory bandwidth
    • A100, H100, B200: server-grade, fast, expensive
    • 3090, 4090, A6000: consumer-grade, still pretty fast, cheaper
  • TPU: Google’s tensor processing unit, optimized for matrix operations
  • Cerebras, Groq: Specialized hardware for LLMs, high memory bandwidth

Training Language Models

  • Train on large corpora of text
  • Goal: learn parameters \(\theta\) such that \(P_\theta(x)\) approximates the true distribution
  • Use maximum likelihood estimation (MLE)
    • \(\theta^* = \arg\max_\theta \sum_{x\in\mathcal D} \log P_\theta(x)\)

Training Steps

  • Forward pass: compute \(P_\theta(x)\)
  • Backward pass: compute gradients \(\nabla_\theta \log P_\theta(x)\)
  • Parameter update: \(\theta \leftarrow \theta + \eta \nabla_\theta \log P_\theta(x)\)
    • \(\eta\) is the learning rate
  • Practically: process large batches of text w/ tensor operations

Training Illustration

Inference with Language Models

  • Given a prompt \(x\), generate a continuation \(y\)
  • Two main approaches:
    • Sampling: draw samples \(y' \sim P_\theta(y \mid x)\)
    • Search: approximately find \(\hat{y} \leftarrow \arg\max_y s_\theta(y \mid x)\)
      • \(s\) may or may not be \(P\)

Inference Illustration

Basic Generation

  • Also called “decoding” (from information theoretic roots).
  • Often done one token at a time, autoregressively. Simplified view:
def generate(model: Model, x: list[Token]):
    y = []
    while not done(y):      # while termination condition not reached
        p = model(x + y)    # get P(y | x)
        y.append(sample(p)) # sample or search for next token
    return y
  • We will cover many variants in this course!

Meta-generation

  • A class of algorithms that generate token sequences as a subroutine.
  • Most common: reranking.
def generate_and_rerank(model: Model, reranker: Reranker, candidate_count: int, x: list[Token]):
    # generate candidate_count candidates
    candidates = [generate(model, x) for _ in range(candidate_count)]
    # score each with the reranker
    scores = [reranker(x, y) for y in candidates]
    # return the highest-scoring candidate
    return candidates[argmax(scores)]
  • We will cover many other algorithms!

Latent Variables

  • Sometimes we want to model things other than the actual answer.
  • Most common: chain of thought.
Variable Example
Input \(x\) “How many years since the Transformer paper was published?”
Latent \(z\) “Now is 2025 and the Transformer paper was published in 2017. 2025 - 2017 = 8.”
Output \(y\) “It has been 8 years since the Transformer paper was published.”
  • Latent variables pose many issues! (efficiency, marginalization)

Evaluation of Inference Outputs

  • We don’t want high-probability outputs, we want good outputs
  • Human Preference: Ask humans to judge outputs according to a rubric
  • LLM as a Judge: Ask an LLM to evaluate outputs according to a rubric
  • Deterministic Metrics: accuracy, BLEU, ROUGE, etc.
  • Also called “reward” in reinforcement learning, \(r(y \mid x)\)

Search Errors vs. Model Errors

  • Search Error: Search algorithm fails to find output w/ highest model score
    • \(s(\text{generate}(\theta, x) \mid x) < \max_y s_\theta(y \mid x)\)
    • Can be mitigated by better inference
  • Model Error: The model scores a worse output better than the best output
    • \(\hat{y} = \arg\max_y s_\theta(y \mid x)\)
    • \(r(\hat{y} \mid x) < \max_y r(y \mid x)\)
    • Can be mitigated by better model training or inference
  • Know which one you are facing!

Diversity vs. Quality

  • Argmax search gives low diversity, sometimes higher quality
  • Sampling gives high diversity, sometimes lower quality

Recap: Inference Desiderata

  • Good evaluation scores
  • Low latency
  • High throughput
  • High diversity
  • Depending on the application, priorities may vary!

This Course: 1. Inference Basics

  • Introduction to Language Models and Inference
  • Probability Review and Shared Task Introduction
  • Common Sampling Methods for Modern NLP
  • Beam Search and Variants
  • Intro to A* and Best First Search
  • Other Controlled Generation Methods

This Course: 2. Reasoning, Tool Use, and Agents

  • Chain of Thought and Intermediate Steps
  • Self-Refine and Self-Correction Methods
  • Reasoning Models
  • Incorporating Tools
  • Agents and Multi-Agent Communication

This Course: 3. Scaling Inference Time Compute

  • Minimum Bayes Risk and Multi-Sample Strategies
  • Reward Models and Best-of-N
  • Systems not Models
  • Inference Scaling vs Model Size
  • Using External Verifiers
  • Token Budgets and Training-Time Distillation

This Course: 4. System-Level Optimization

  • Defining Efficiency
  • Library Implementations and Optimizations
  • Prefix Sharing and KV Cache Optimizations
  • Draft Models and Speculative Decoding
  • Linearizing Attention and Sparse Models
  • Transformer Alternatives

What Won’t We Cover?

  • Model training is limited (only together w/ inference)
  • Model architectures are limited
  • Model evaluation is limited
  • Inference on non-text data is limited

Grading

  • 15% Quizzes (given most weeks)
  • 60% Assignments (3 total)
  • 25% Final Project

Shared Tasks

  • 3 tasks that can be solved with language models
    • Mathematical reasoning
    • Multiple choice question answering
    • Open-ended generation
  • Details to be released soon

Assignments and Schedule

  • HW1: generation algorithms
  • HW2: meta-generation algorithms
  • HW3: hardware & optimization
  • Final Project: inference server

Questions + Discussion

Carnegie Mellon University - Language Model Inference - Fall 2025